Sistem bilangan di dalam dunia komputer

Sistem bilangan di dalam dunia komputer

Sistem Bilangan atau Number System adalah Suatu cara untuk mewakili besaran dari suatu item fisik. Sistem Bilangan menggunakan suatu bilangan dasar atau basis (base / radix) yang tertentu. Dalam hubungannya dengan komputer.

1. Desimal (Basis 10)

Desimal (Basis 10) adalah Sistem Bilangan yang paling umum digunakan dalam kehidupan sehari-hari. Sistem bilangan desimal menggunakan basis 10 dan menggunakan 10 macam simbol bilangan yaitu : 0, 1, 2, 3, 4, 5, 6, 7, 8 dan 9. Sistem bilangan desimal dapat berupa integer desimal (decimal integer) dan dapat juga berupa pecahan desimal (decimal fraction).

Untuk melihat nilai bilangan desimal dapat digunakan perhitungan seperti berikut, misalkan contoh bilangan desimal adalah 8598. Ini dapat diartikan :

Dalam gambar diatas disebutkan Absolut Value dan Position Value. Setiap simbol dalam sistem bilangan desimal memiliki Absolut Value dan Position Value. Absolut value adalah Nilai Mutlak dari masing-masing digit bilangan. Sedangkan Position Value adalah Nilai Penimbang atau bobot dari masing-masing digit bilangan tergantung dari letak posisinya yaitu bernilai basis di pangkatkan dengan urutan posisinya. Untuk lebih jelasnya perhatikan tabel dibawah ini.

Dengan begitu maka bilangan desimal 8598 bisa diartikan sebagai berikut :

Sistem bilangan desimal juga bisa berupa pecahan desimal (decimal fraction), misalnya : 183,75 yang dapat diartikan :

2. Biner (Basis 2)

Biner (Basis 2) adalah Sistem Bilangan yang terdiri dari 2 simbol yaitu 0 dan 1. Bilangan Biner ini di populerkan oleh John Von Neumann. Contoh Bilangan Biner 1001, Ini dapat di artikan (Di konversi ke sistem bilangan desimal) menjadi sebagai berikut :

Position Value dalam sistem Bilangan Biner merupakan perpangkatan dari nilai 2 (basis), seperti pada tabel berikut ini :

Berarti, Bilangan Biner 1001 perhitungannya adalah sebagai berikut :


3. Oktal (Basis 8)

Oktal (Basis 8) adalah Sistem Bilangan yang terdiri dari 8 Simbol yaitu 0, 1, 2, 3, 4, 5, 6, 7.Contoh Oktal 1024, Ini dapat di artikan (Di konversikan ke sistem bilangan desimal) menjadi sebagai berikut :
Position Value dalam Sistem Bilangan Oktal merupakan perpangkatan dari nilai 8 (basis), seperti pada tabel berikut ini :


Berarti, Bilangan Oktal 1022 perhitungannya adalah sebagai berikut :

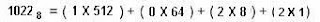
4. Hexadesimal (Basis 16)

Hexadesimal (Basis 16), Hexa berarti 6 dan Desimal berarti 10 adalah Sistem Bilangan yang terdiri dari 16 simbol yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15). Pada Sistem Bilangan Hexadesimal memadukan 2 unsur yaitu angka dan huruf. Huruf Amewakili angka 10, B mewakili angka 11 dan seterusnya sampai Huruf F mewakili angka 15. 

Contoh Hexadesimal F3D4, Ini dapat di artikan (Di konversikan ke sistem bilangan desimal) menjadi sebagai berikut :

Position Value dalam Sistem Bilangan Hexadesimal merupakan perpangkatan dari nilai 16 (basis), seperti pada tabel berikut ini :

Berarti, Bilangan Hexadesimal F3DA perhitungannya adalah sebagai berikut :

5. Bilangan Hexa

Bilangan Hexa adalah sistim bilangan yang berbasis 16, artinya sistim bilangan hexa mengenal angka 0 sampai dengan 15. Hal ini berbeda dengan bilangan desimal yang merupakan bilangan berbasis 10 dan menggunakan angka 0 sampai 9 untuk menandai nilai bilangan hexa dimulai dari 0 sampai 9 dan dilanjutkan A sampai F untuk menyatakan nilai bilangan 10 sampai 15 bilangan desimal berikutnya.

Sebagai contoh pembanding cara penulisan antara bilangan Desimal, Hexa dan Biner, kita perhatikan tabel berikut di bawah ini

Desimal	Hexa	Biner
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Konversi Bilangan Hexa ke Desimal

Untuk mengkonversi bilangan hexa ke desimal dapat dilakukan dengan mudah, yaitu seperti yang kita lakukan pada cara konversi biner ke desimal. Setiap tingkatan harga bilangan oktal 0 sampai dengan F dikalikan dengan pengali dan dijumlahkan, maka akan didapatkan harga desimalnya.

Berikut merupakan contoh konversi bilangan hexa 309 ke desimal ternyata didapatkan hasil 777.

65536		4096		256		16		1		Pengali
164		163		162		161		160		Tingkatan
				3		0		9		Bilangan
				3×256	+	0×16	+	9×1
				768	+	0	+	9	=	777

Konversi Bilangan Desimal ke Hexa

Dalam melaksanakan konversi dari Desimal ke Hexa kita dapat menggunakan daftar konversi berikut sebagai dasar konversi.

Desimal	Hexa	164	163	162	161	160
1	1	65 536	4 096	256	16	1
2	2	131 072	8 192	512	32	2
3	3	196 608	12 288	768	48	3
4	4	262 144	16 384	1 024	64	4
5	5	327 680	20 480	1 280	80	5
6	6	393 216	24 576	1 536	96	6
7	7	458 752	28 672	1 792	112	7
8	8	524 288	32 768	2 048	128	8
9	9	589 824	36 864	2 304	144	9
10	A	655 360	40 960	2 560	160	10
11	B	720 896	45 056	2 816	176	11
12	C	786 432	49 152	3 072	192	12
13	D	851 968	53 248	3 328	208	13
14	E	917 504	57 344	3 584	224	14
15	F	983 040	61 440	3 840	240	15

Sebagai contoh kita akan mengkonversi bilangan desimal 1983 ke bilangan hexa,

1983 – 1792	sisa 191 (dari daftar 1792 adalah 7 hexa pada tingkat 162)
191 – 176	sisa 15 (dari daftar 176 adalah B hexa pada tingkat 161)
15 – 15	sisa 0 (dari daftar 15 adalah F hexa pada tingkat 160)
Maka hasil konversinya diperoleh 7 B F hexa.atau dapat ditulis 7BF(16)

Konversi Biner ke Hexa

Cara mengkonversi bilangan biner ke bilangan hexa dapat dilakukan dengan cara mengelompokan bilangan biner menjadi empat-empat digitnya, kemudian kita tuliskan nilai konversinya ke bilangan hexa dari empat digit kelompok bilangan biner tersebut maka kita sudah mendapatkan konversi biner ke hexa.

Perhatikan contoh dibawah ini, kita akan mengkonversi bilangan biner 1001 1011 1100₍₂₎ ke bilangan hexa maka didapatkan hasil sebagai berikut :

1001	1011	1100	Biner (1001 1011 1100)2
9	B	C	Hexa (9BC)16

Demikian juga bila kita ingin mengkonversikan bilangan hexa ke bilangan biner, dapat dilakukan dengan cara memisahkan masing-masing bilangan hexa kemudian mengkonversikan bilangan oktal tersebut ke bilangan biner.

F	8	C	Hexa (F8C)16
1111	1000	1100	Biner (1111 1000 1100)2